Um estudo sobre as raízes n-ésimas da unidade.

Resumo

Este trabalho apresenta parte dos estudos realizados durante as atividades do Projeto de Pesquisa “Decaimento de soluções de Equações de Meios Porosos com termos advectivos”, que ocorreram durante o primeiro semestre de 2019 no IFRS - campus Canoas. Este projeto é conduzido por dois estudantes bolsistas que são auxiliados por um professor coordenador do projeto. Resumidamente, os bolsistas fazem pesquisas bibliográficas a respeito de diversos temas relacionados a matemática e apresentam suas conclusões para o professor orientador e também para estudantes interessados. Durante o presente ano, os bolsistas estão pesquisando sobre Teoria dos Grafos e assuntos correlatos. Deste tema bastante abrangente, há várias linhas de pesquisa. Por exemplo, um dos bolsistas optou por estudar abordagens de Teoria de Grafos no ensino médio e eu escolhi estudar propriedades de grafos relacionadas à Álgebra Linear.  Nesse sentido, pretendo trazer uma discussão a respeito das raízes n-ésimas da unidade, abordando a multiplicação de números complexos em sua forma trigonométrica [z = ρ(cos θ + i · sem θ)], para então deduzir a primeira  (zⁿ = ρⁿ [cos (nθ) + i · sem (nθ)]) e a segunda Lei de Moivre( 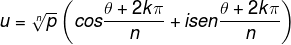). Com este trabalho, queremos mostrar que todo número complexo não nulo z apresenta, de fato, n raízes n-ésimas e que tais raízes são os vértices de um polígono regular de n lados, inscrito na circunferência de raio igual a raiz n-ésima do módulo de z e centrada na origem do Plano Complexo. O estudo desses conteúdos sobre números complexos é importante, por exemplo, para melhor entendermos a Teoria Espectral (Teoria esta que busca analisar as propriedades estruturais de grafos através de matrizes e seus espectros, ou seja, dos autovalores das matrizes associadas a eles) das matrizes circulantes e de outras matrizes de adjacência de grafos que possuem autovalores complexos e/ou autovetores com entradas complexas.